2 de diciembre del 2016
Clase #12
Eventos Independientes
Definición:
Sean A y B eventos independientes entonces se cumple:
P(A∩B) = P(A) P(B)
9 de diciembre del 2016
Clase #13
En esta clase se realizó la evaluación 2, cuya corrección la podrán encontrar en Evidencias, esta prueba contenía temas de muestras bivariadas y probabilidad.
SEGUNDO BIMESTRE
13 de diciembre del 2016
Clase #1
Variables Aleatorias
Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral S un número real.
Se utilizan letras mayúsculas,por lo general las últimas: X, Y, ...; para designar variables aleatorias, y las respectivas minúsculas (x, y, ...) para designar valores concretos de las mismas.
Se clasifican en:
- Variables Aleatorias Discretas
- Variables Aleatorias Continuas
Variables Aleatorias Discretas
Sean: X: Variable aleatoria
S: Espacio muestral
S: Espacio muestral
e: Evento
x: Valor que puede tomar X
R: conjunto de los números reales
R: conjunto de los números reales
entonces,
X: S → R
e → X
e → X
es la correspondencia que establece la variable aleatoria X.
dom X = S
rang X ϵ S
Ejemplos:
1. En un experimento se lanzan 3 monedas y se observa el resultado, describa el espacio muestral para este experimento y describa una variable aleatoria para el número de sellos que se obtiene.
c: cara Experimento: lanzamiento de 3 monedas.
s: sello
S = {ccc, scc, csc, ccs, ssc, scs, css, sss}
x = {0, 1 ,2 ,3} = rang X
Y= Diferencia entre número de caras y sellos
y = {3, 1, -1, -3} = rang Y
Z= Número de caras al cubo más el doble del número de sellos
z = {27, 10, 5, 6}= rang Z
2. En un experimento se lanza repetitivamente una moneda. Determine el rango y el tipo de variable aleatoria discreta.
Experimento: Lanzar una moneda repetitivamente
X: Cantidad de lanzamientos realizados hasta que salga un sello
S ={s, cs, ccs, cccs, ccccs,.....}
x = {1 ,2 ,3, 4,.......} = rang X
Sea X una variable aleatoria discreta (v.a.d), entonces P(X = x) representa la probabilidad de que la v.a.d para q tomo el valor de x.
Sean: X = v.a.d
f(X) = P(X = x)
entonces,
f: X → R
x → P(X = x)
Propiedades:
1. ꓯx / f(x) ≥ 0
2. Ʃ f(x) = 1
Ejemplos:
1. Para el ejemplo de lanzamiento de las 3 monedas . Determine la función de distribución de la probabilidad.
FUNCIÓN DE DISTRIBUCIÓN DE PROBABILIDAD
Sea X una variable aleatoria discreta (v.a.d), entonces P(X = x) representa la probabilidad de que la v.a.d para q tomo el valor de x.
Sean: X = v.a.d
f(X) = P(X = x)
entonces,
f: X → R
x → P(X = x)
Propiedades:
1. ꓯx / f(x) ≥ 0
2. Ʃ f(x) = 1
Ejemplos:
1. Para el ejemplo de lanzamiento de las 3 monedas . Determine la función de distribución de la probabilidad.
Descripción:
Representa la función de distribución de la probabilidad del experimento del lanzamiento de las 3 monedas.
Representa la función de distribución de la probabilidad del experimento del lanzamiento de las 3 monedas.
Interpretación:
Se puede observar que los datos están distribuidos simétricamente.
Se puede observar que los datos están distribuidos simétricamente.
2. En un lote de 5 artículos, 3 son defectuosos y 2 aceptables. Se toma una muestra aleatoria sin reemplazo de 2 artículos encuentre la distribución de probabilidad de la variable aleatoria, cantidad de artículos defectuosos que se obtiene en la muestra.
Experimento: Extracción de 2 artículos sin reemplazo.
X: Cantidad de artículos defectuosos.
a b c: Artículos defectuosos.
d e: Artículos aceptables.
S= {(a,b); (a,c); (b,c); (a,d); (a,e); (b,d); (b,e); (c,d); (c,e); (d,e)}
n=10
Experimento: Extracción de 2 artículos sin reemplazo.
X: Cantidad de artículos defectuosos.
a b c: Artículos defectuosos.
d e: Artículos aceptables.
S= {(a,b); (a,c); (b,c); (a,d); (a,e); (b,d); (b,e); (c,d); (c,e); (d,e)}
n=10
Descripción:
Representa la función de distribución de la probabilidad del experimento de la extracción de 2 artículos sin reemplazo.
Interpretación:
Se puede observar que los datos no están distribuidos simétricamente.
Ejemplo:
Determine:
a) F(X)
b) F(2,5) = P(X ≤ 2,5) =7/8
c) F(-3,4) = P(X ≤ -3,4) = 0
d) F(24,7) = P(X ≤ 24,7) = 1
e) P(X>2,5) = 1- P(X ≤ 2,5) = 1-7/8 = 1/8
Ejemplos:
1. Determinar la esperanza para el exprimento del lanzamiento de las 3 monedas.
VARIANZA
Sea X: v.a.d
f(X): Distribución de probabilidad de X
V(X) = σ2(X) = Varianza de X
entonces,
VITUTOR. (2014). Variable Aleatoria. Disponible en: http://www.vitutor.com/pro/3/a_1.htmlSe puede observar que los datos no están distribuidos simétricamente.
16 de diciembre del 2016
Clase #2
DISTRIBUCIÓN DE PROBABILIDAD ACUMULADA
Sean X: v.a.d
f: Distribución de probabilidad
F: Distribución de probabilidad acumulada
entonces,
F(X) = P(X=x) = Ʃ f(x)
F: R → R
dom F: R
rang F: C[0,1]
Propiedades:
1. lim X→-∞ F(X)=0 y lim X→+∞ F(X)=1
2. 0 ≤ F(X) ≤ 1
3. a < b → F(a) < F(b)
4. P(X>a) =1 → P(X ≤ a) =1 - F(a)
Ejemplo:
Determine:
a) F(X)
b) F(2,5) = P(X ≤ 2,5) =7/8
c) F(-3,4) = P(X ≤ -3,4) = 0
d) F(24,7) = P(X ≤ 24,7) = 1
e) P(X>2,5) = 1- P(X ≤ 2,5) = 1-7/8 = 1/8
ESPERANZA Y VARIANZA DE UNA VARIABLE ALEATORIA DISCRETA
ESPERANZA
Sean X: v.a.d
Sean X: v.a.d
f(X): Distribución de probabilidad de X
u = E(X) = Media o valor esperado de X
entonces,
u = E(X) = Ʃ x . f(X)
Propiedades:
1. E(c) = c; donde c = constante
2. E(cX) = c . E(X)
3. E(X + Y) = E(X) + E(Y)
4. Si Y = aX + b; donde a, b = constantes y X,Y = v.a.d
entonces,
E(Y) = E(aX) + E(b)
E(Y) = a . E(X) + b
Ejemplos:
1. Determinar la esperanza para el exprimento del lanzamiento de las 3 monedas.
uX = E(X) = Ʃ x . f(x)
E(X) = 0* 1 + 1* 3 + 2* 3 + 3* 1
8 8 8 8
E(X) = 3
2
20 de diciembre del 2016
Clase #3
VARIANZA
Sea X: v.a.d
f(X): Distribución de probabilidad de X
V(X) = σ2(X) = Varianza de X
entonces,
V(X) = σ2(X) = E(X- uX)2 = Ʃ (X- uX)2 . f(X)
V(X) = E(X2) - uX2 = E(X2) - (E(X))2
Propiedades:
1. V(c) = 0, donde c = constante
2. V(cX) = c2 . V(X)
3. V(X + Y) = V(X) + V(Y), donde X,Y = v.a.d
DESVIACIÓN ESTÁNDAR
σX = √V(X)
Ejemplos:
1. Una persona quiere abrir una puerta y tiene 5 llaves de las cuales solo una corresponde a la cerradura, la persona va eligiendo al azar y probando abrir la puerta. Calcular la esperanza y la varianza del número de intentos si se separa las llaves que probó anteriormente.
Variables Aleatorias Continuas
Definición:
- La variable cuyo recorrido es un intervalo finito o infinito de R se llama variable aleatoria continua (v.a.c).
- También se dice que X es una v.a.c si:
P(X=x) = 0
- Sea X: v.a.c
La función real F, tal que:
REFERENCIAS
La función real F, tal que:
ꓯt ϵ R, F(t) = P(X ≤ t)
Se denomina la función de distribución de la variable aleatoria X.
Propiedades:
Propiedades:
1. F es creciente
lim X→-∞ F(X)=0 y lim X→+∞ F(X)=1
2. P(a ≤ X ≤ b) = P(a < X < b) = P(a ≤ x < b) = P(a < X ≤ b)
FUNCIÓN DE DENSIDAD
La función de densidad de una v.a.c. X es una función real f, tal que:
i) f(X) = 0
iii) Para cualquier intervalo A= [a,b]; se tiene:REFERENCIAS
NAVIDI, W., (2006). Estadística para ingenieros y científicos. The MacGraw-Hill. México, D.F.







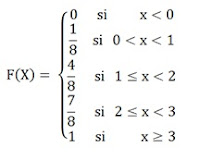







No hay comentarios:
Publicar un comentario