Octubre

11 de octubre del 2016

Clase #1

Indicaciones Iniciales

En esta primera clase se dieron indicaciones como:

1. Crear una cuenta en gmail.

2. Hacer un blog acerca de un portafolio estudiantil personal de Probabilidad y Estadística, en cual se detalle lo hecho en cada clase.

A su vez se trató el tema de los valores que debemos tener entre profesor y estudiante, como es el respeto, responsabilidad, puntualidad, honestidad, compañerismo, entre otros que son muy importantes al igual que los nombrados anteriormente.

"Tus creencias se convierten en tus pensamientos, tus pensamientos se convierten en tus palabras, tus palabras se convierten en tus acciones, tus acciones se convierten en tus hábitos, tus hábitos se convierten en tus valores, tus valores se convierten en tu destino". 

Mahatma Gandhi

PRIMER BIMESTRE

14 de octubre del 2016

Clase #2

Capítulo #1

Muestreo y Estadística Descriptiva

OBJETIVOS DE ESTUDIO:

1.Determinar los ámbitos de aplicación e importancia del estudio de la estadística.

2.Estudiar las definiciones básicas de muestreo y estadística descriptiva.

3.Describir los procesos de recopilación, tabulación y representación gráfica de los datos.

4.Calcular e interpretar los principales parámetros estadísticos.

ESTADÍSTICA

La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

La estadística tiene dos partes significativas:

ESTADÍSTICA DESCRIPTIVA

Su objetivo principal es el de conocer e interpretar los datos obtenidos en un determinado estudio o experimento.

Un estudio estadístico consta de las siguientes fases:

• Recogida y estandarización de datos.
• Organización y representación de datos.
• Análisis e interpretación de datos.
• Obtención de conclusiones.

Métodos de Obtención de Datos: Encuesta, entrevistas, base de datos, entre otros.

POBLACIÓN Y MUESTRA

Población (universo): Tamaño (N)
Muestra: Tamaño (n)

M ⊂ P
n ≤ N

Ejemplo P = M
Es el censo.



Muestra aleatoria simple: de tamaño n es una muestra elegida por un método en el que cada colección de n elementos de la población tiene la misma probabilidad de formar la muestra. Ej.: La lotería.

Muestra de conveniencia: es una muestra que no se extrae por un método aleatorio bien definido.

VARIABLES:

25 de octubre del 2016

Clase #3

Escalas de Medida

Es un instrumento con el que se asignan valores a una unidad estadística

Nominal:
Se asignan números a las variables, pero solo como una forma de codificación . Sirve más para identificar variables cualitativas.

         Ejemplos:

a) Hombres    0                                Variable: Sexo
    Mujeres      1

b) Soltero         0                            Variable: Estado Civil
    Casado         1
    Divorciado   2
    Unión libre  3

Ordinal:

Se asigna orden a los valores de la variable medida, es decir se tiene una clasificación en orden jerárquica. Sirve más para identificar variables cualitativas.

         Ejemplos:

a) Excelente                                    Variable : Atención al cliente
    Buena

    Regular

b) Excelente                                   Variable : Rendimiento Académico
    Muy buena  
    Regular        
    Insuficiente    

Escala de Intervalo:
Si se asignan valores dentro de un intervalo finito o infinito con la particularidad que existe un “cero relativo”. 

         Ejemplos:

a) Variable : Temperatura en grados centígrados

b) Variable : Puntuación en un examen

Escala de Razón:
Si se asignan valores dentro de un intervalo finito o infinito con la particularidad que existe un “cero absoluto”.

         Ejemplos:

a) Variable: Temperatura en grados kelvin

b) Variable: Estatura de una persona

c) Variable: Tiempo de vida útil de un equipo


VALORES ATÍPICOS

Medición de Temperaturas

Dato no común que está por encima y por debajo del resto, es decir se encuentran muy alejados de la medida, se pueden generar varios errores.

Se pueden excluir siempre y cuando sea verificado cuál fue el motivo de la medida atípica, es decir cuál fue el error, por lo que se tendría que analizar por separado.

CARACTERÍSTICAS DE LOS DATOS

Localización:
- La posición relativa de los datos con respecto de los otros.
  Se forman grupos o nubes.

Dispersión: 
- La variación entre los valores medidos alrededor de la media.
- Se pretende medir el grado de diseminación de los datos alrededor de la media.

Ejemplo:
En el caso de la manufactura, una alta precisión está asociada con una baja dispersión.

Entre más lejos más dispersión
Baja la precisión

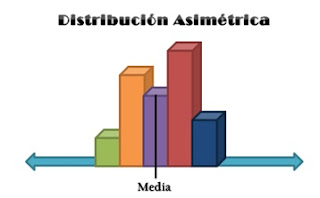
Simetría:

Si los valores de la variable están distribuidos de forma similar por encima y por debajo de la media.

Distribución de Frecuencias

- Sirve para resumir en una tabla numerosos datos de manera que se pongan de manifiesto las características de los datos.
-Se utiliza para resumir datos cualitativos nominales u ordinales.
-Si los datos son cuantitativos continuas se debe previamente formar intervalos o clases.
-Se entiende por “frecuencia absoluta”, al número de veces que se repite un valor en un conjunto de datos y se simboliza con “ni”.
-Si la muestra es de tamaño “n”, entonces:

n= n1 + n2 +….+nk

                                                                   n= ∑ ni

PROCEDIMIENTO

I) DATOS CUANTITATIVOS

  a) Individuales

1. Ordenar en forma ascendente los datos.
2. Colocar las frecuencias absolutas de cada dato.
3. Calcula la “frecuencia relativa” que se simboliza “fi”.

                                           
4. Calcular las frecuencias acumuladas (Ni) y frecuencias relativas acumulado (Fi).
                                                                       

REFERENCIAS
MORALES, R.  Estadística. Disponible en: http://www.monografias.com/trabajos93/sobre-estadistica/sobre-estadistica.shtml.
NAVIDI, W., (2006). Estadística para ingenieros y científicos. The MacGraw-Hill. México, D.F.